Broschiertes Buch

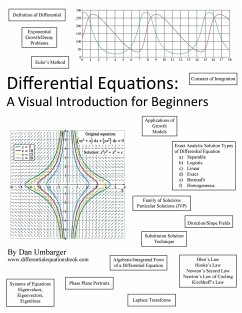
Partial Differential Equations in Fluid Mechanics

Beschreibung

A selection of survey articles and original research papers in mathematical fluid mechanics, for both researchers and graduate students.

Produktdetails

• Verlag: Cambridge University Press
• Seitenzahl: 340
• Erscheinungstermin: 22. Februar 2019
• Englisch
• Abmessung: 229mm x 152mm x 20mm
• Gewicht: 553g
• ISBN-13: 9781108460965
• ISBN-10: 1108460968
• Artikelnr.: 53166284