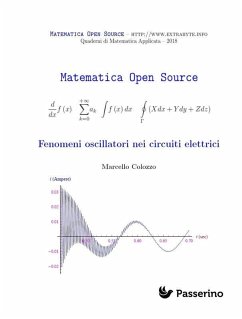
Nei due ultimi ebooks abbiamo gettato le basi per lo studio dei cosiddetti "fenomeni oscillatori". Precisamente, abbiamo trattato la serie di Fourier e l'oscillatore armonico in Meccanica classica. Come ben si espresse il fisico russo Felix Ruvimovich Gantmacher nel suo libro "Meccanica analitica", esistono delle analogie elettromeccaniche nel senso che il passaggio da processi oscillatori meccanici a processi oscillatori nei circuiti elettrici, conserva la forma delle equazioni differenziali. Più precisamente, la massa inerziale m di una particella vincolata a una molla di costante elastica k, ha come "controparte elettrica" il coefficiente di autoinduzione L. Il reciproco 1/k della costante elastica diviene la capacità C di un condensatore in serie all'induttanza, mentre alla resistenza viscosa corrisponde la resistenza ohmica R. In tal modo l'oscillatore armonico esibisce un'analogia formale con un circuito costituito da una resistenza R, un'induttanza L e un condensatore di capacità C. L'ascissa della particella diviene, invece, la carica elettrica sulle armature del condensatore. Possiamo dunque scrivere un'equazione differenziale (che ovviamente può essere ricavata applicando i principi di Kirchoff, i quali vengono richiamati nel capitolo 1) e assegnare un appropriato problema di Cauchy, la cui soluzione mostra l'esistenza di fenomeni transienti. Il vantaggio di tale paradigma rispetto alla scrittura delle impedenze complesse, risiede proprio nel fatto che offre la possibilità di studiare i predetti processi transitori, come mostrato nel grafico di copertina. D'altra parte, le equazioni differenziali in istudio parlano il "linguaggio" dei sistemi dinamici (limitando l'esame ai sistemi lineari). Come è ben noto, la linearità conduce al "principio di sovrapposizione" che consente l'applicazione dell'analisi di Fourier. Si tratta, dunque, di un paradigma estremamente potente, in quanto permette lo studio del comportamento di una rete alimentata da una d.d.p che non sia necessariamente sinusoidale e più in generale, periodica. Marcello Colozzo, laureato in Fisica si occupa sin dal 2008 di didattica online di Matematica e Fisica attraverso il sito web Extra Byte dove vengono eseguite "simulazioni" nell'ambiente di calcolo Mathematica. Negli ultimi anni ha pubblicato vari articoli di fisica matematica e collabora con la rivista Elettronica Open Source. Appassionato lettore di narrativa cyberpunk, ha provato ad eseguire una transizione verso lo stato di "scrittore cyber", pubblicando varie antologie di racconti.
Dieser Download kann aus rechtlichen Gründen nur mit Rechnungsadresse in A, B, BG, CY, CZ, D, DK, EW, E, FIN, F, GR, HR, H, IRL, I, LT, L, LR, M, NL, PL, P, R, S, SLO, SK ausgeliefert werden.
Hinweis: Dieser Artikel kann nur an eine deutsche Lieferadresse ausgeliefert werden.